菜百投资金条今日价格(菜百投资金条今日价格实时更新)
alicucu 2025-12-31 06:59 2 浏览
存哪也不要存银行。
1,金条就是去黄金公司买,银行也有。金条一般是紧跟黄金市场的趋势报价销售,以及回购。
2,关于回购你要问清,是否回购,回购价格,黄金涨多少我就能回本。
商品 最新价格 菜百今日金价 288元/克 菜百今日黄金价格 288元/克 菜百足金价格 285元/克 菜百千足金价格 288元/克 菜百摆件价格 335元/克 菜百饰品金条价格 280元/克 菜百铂金价格(Pt950) 337元/克 菜百铂金价格(Pt990) 350元/克 菜百千足铂价格 360元/克 菜百投资金条价格 240.5元/克 菜百投资银条价格 3.44元/克
菜百小金条通常是指重量为1克的金条,因此它的重量是1克。这种小金条通常是用于投资、收藏或赠送礼物的,其外观精美,质量可靠。虽然小金条的重量相对较小,但它仍然具有保值、升值的潜力,特别是在经济不稳定的时期,黄金的价值更加凸显。菜百小金条因其精美的外观和实用性备受欢迎,是一种非常适合投资者和收藏家的黄金产品。
菜百最小金条5克,质量非常好。
菜百的金条在一定程度上具有保值潜力。首先,菜百作为一家信誉良好、品牌认知度高的企业,其推出的金条产品在市场上具有一定的竞争优势。
其次,黄金作为一种传统的保值投资工具,历来受到人们的追捧。尤其是在经济不确定的时期,人们更倾向于将资金投入到相对稳定的金融产品中以规避风险。因此,从这些方面来看,菜百的金条具有一定的保值和升值潜力。然而,投资任何形式的黄金都需要谨慎,投资者应该根据自己的风险承受能力和投资目标进行合理的投资决策。
黄金在一定程度上能起到保值的作用,但不是万能的。比较稳定,不是绝对的。投资理财是要有风险的ⅰ祝你好运丶
相关推荐
- 东北发生的五件真实灵异事件
-
下辈子的依恋作者:楚叶的梦简介:这辈子的恋情都没有结束了,结果就变成下辈子的依恋了,到底是为什么,上辈子都没有办法忘记你,这辈子我又恋上了你,真是悲剧啊!第一本:《我是一个封鬼师》作者:灵梟精...
- 乒乓球起源哪个国家(乒乓球起源于哪里)
-
乒乓球起源于英国,不是日本。19世纪末,欧洲盛行网球运动,但由于受到场地和天气的限制,英国有些大学生便把网球移到室内,以餐桌为球台,用羊皮纸做球拍。1890年,英国运动员吉布从美国带回一些赛璐珞球,用...
-
- 应届生简历模板(应届生简历模板word个人简历)
-
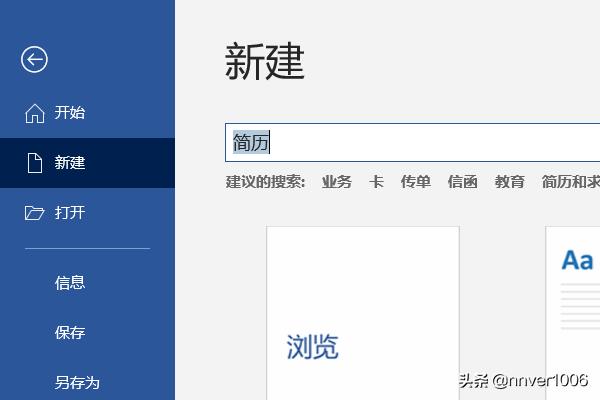
个人简历模板如何下载word格式?其实word本身就自带比较多的简历模板,可以直接在word上查找后直接下载即可,下面就跟大家分享一下具体的步骤:1、首先打开一个空白的word文档,点击左上角的“文件”-“新建”,然后在搜索栏中输入简历,查...
-
2025-12-31 12:12 alicucu
-
- 怎么查询邮政快递到哪里了(怎么查询邮政快递到哪里了呢)
-
步骤/方式1微信搜索邮政快递小程序。步骤/方式2在邮政快递小程序页面点击下单查快递。步骤/方式3输入单号就可以查询快递具体位置信息。1.官网,通过EMS官网对快件进行跟踪,相关信息可以直接通过快递回执上的条形码进行查询,即可在公司的网页上输...
-
2025-12-31 11:59 alicucu
- 欧尼桑(欧尼桑动漫免费观看)
-
欧尼桑:哥哥此外,同意是音译过来的有:欧奈桑:姐姐欧卡阿桑:妈妈欧巴桑:阿姨、姑姑欧巴阿桑:奶奶、外婆欧拖桑:爸爸欧吉桑:叔叔、伯伯欧吉意桑:爷爷、外公欧尼桑:哥哥此外,同意是音译过来的有:欧奈桑:...
- 湄洲湾职业技术学院(湄洲湾职业技术学院在哪里)
-
公交线路:k02路→102路,全程约30.3公里1、从莆田市步行约530米,到达市政府站2、乘坐k02路,经过5站,到达市公交南站(也可乘坐k03路)3、乘坐102路,经过26站,到达湄洲湾技...
- 黑龙江工业学院官网(黑龙江工业学院官网招生办电话)
-
黑龙江工业学院成立于2013年4月,前身是鸡西大学。是经教育部批准的本科建制学院,2021年该校设有电器与信息工程学院,环艺与建筑工程学院,现代制造工程学院,资源工程学院,经济管理学院,国际教育学院,...
- 鬼新娘图片(《邪神墨然》鬼新娘图片)
-
杨帆(1943-2006),60、70年代香港邵氏电影著名男演员,生于1943年,出生于四川,在台湾长大,“国立艺专”影剧科毕业,1966年赴港加入邵氏电影公司,首次在琼瑶同名小说改编的电影《船》(1...
-
- 晚清四大奇案是什么(晚清4大悬案)
-
清末四大奇案之所以奇,主要是奇在案情复杂,而且探案的过程也是十分的曲折,结果更是让人怎么想也是想不到的,因此清末这四大奇案也是为世人所津津乐道的,它们各有各的特点。首先排第一名的案件就是刺马案,刺马案是当年在曾国藩调离江宁之后,朝廷派了一个...
-
2025-12-31 09:12 alicucu
- 贝加尔湖歌曲(贝加尔湖歌曲简谱)
-
《贝加尔湖》歌词如下:在我的怀里在你的眼里,那里春风沉醉那里绿草如茵,月光把爱恋洒满了湖面,两个人的篝火照亮整个夜晚,多少年以后如云般游走,那变换的脚步让我们难牵手,这一生一世有多少你我...
-

- 惠普官网驱动下载(惠普官网驱动下载步骤)
-
1/6登陆www.hp.com.cn,点击右上角的“支持”,选择“软件与驱动程序”2/6点击左侧“按产品类别浏览”中的“打印机”3/6输入要查询的产品编号4/6点击左侧搜索结果中的目标打印机5/6点击右下角选项2中的搜索6/6...
-
2025-12-31 08:12 alicucu
- 博客登录首页(博客登录官网)
-
若要登录五一博客个人主页,首先需要进入五一博客官网。在官网右上角找到“登录”按钮,点击后输入注册时填写的账号和密码,然后点击“登录”按钮即可成功登录个人主页。在个人主页中,可以进行个人信息的编辑、博客...
- 黑鱼价格多少钱一斤(黑鱼目前市场价格)
-
一般顺序是草鱼、鲤鱼、黑鱼依次价格变高各地会有地域性差异黑鱼的药用价值要高些,价格也相对比鲶鱼高,味道没有鲶鱼鲜美,黑鱼皮厚,肉粗。
- 菜百投资金条今日价格(菜百投资金条今日价格实时更新)
-
存哪也不要存银行。1,金条就是去黄金公司买,银行也有。金条一般是紧跟黄金市场的趋势报价销售,以及回购。2,关于回购你要问清,是否回购,回购价格,黄金涨多少我就能回本。商品最新价格菜百今...
- 水龙头热水器哪个牌子好(水龙头速热热水器哪个牌子好)
-
电热水龙头哪个牌子好1、奥特朗奥特朗属于奥特朗电器(广州)有限公司旗下品牌,是我国电热水龙头行业的领先品牌,产品质量出色,拥有多项国家专利技术,一直致力于为消费者提供品质出色的电热水产品。2、传福传福...
- 一周热门
- 最近发表
- 标签列表
-


