花信年华(花信年华最精辟的一句)
alicucu 2026-01-13 09:12 2 浏览
花信年华出自宋代范成大的《元夕后连阴》。 原文是: 问讯东风几日来,冷烟寒雾锁池台。
扫空积雪翻成雨,收尽残灯未见梅。
夜饮厌厌非老伴,春阴漠漠是愁媒。
谁能腰鼓催花信,快打凉州百面雷。 意思是: 想知道春天什么时候来,冷烟寒雾,天地一片寒冬景象。雪过后依旧是雨,想寻梅也寻不到。常常在夜晚饮酒,期待春天到来却还未得。希望有谁能用腰鼓声来催花信的到来。 所谓花信风,就是指某种节气时开的花,因为是应花期而来的风,后来人们常常用来形容年轻貌美的女子,所以也及哦啊做花信年华。
“花信年华”指女子到了二十四岁,正值青春年少、如花绽放的美好时期。“偶得佳缘”意思是偶然间获得了美好的缘分。
整句话的意思是正值青春美好的年纪偶然获得了一段美好的姻缘或感情缘分。
发信年花偶得佳缘的意思是,花季少年觅得有缘的另一半。
相关推荐
- 寒窑赋原文(寒窑赋原文及译文)
-
天有不测风云,人有旦夕祸福。蜈蚣百足,行不及蛇;雄鸡两翼,飞不过鸦。马有千里之程,无骑不能自往;人有冲天之志,非运不能自通。天有不测风云,人有旦夕祸福。蜈蚣百足,行不及蛇;雄鸡两翼,飞不过鸦。马有千里...
- 夹克衫的英文(夹克衫的英文怎么读jacket)
-
jacket释义:n.羽绒滑雪衫;西装短外套;短上衣,夹克;土豆皮;书籍的护封;文件套,公文夹vt.给…穿夹克;给…装护套;给…包上护封;〈口〉打shirt释义:n.衬衫;汗衫,内衣例句:He...
- 花信年华(花信年华最精辟的一句)
-
花信年华出自宋代范成大的《元夕后连阴》。原文是:问讯东风几日来,冷烟寒雾锁池台。扫空积雪翻成雨,收尽残灯未见梅。夜饮厌厌非老伴,春阴漠漠是愁媒。谁能腰鼓催花信,快打凉州百面雷。意思是:想...
- 汶川泥石流视频(汶川泥石流路况最新消息今天)
-
会有,下暴雨时,四川省阿坝州汶川县多处发生泥石流,其中三江镇、水磨镇、银杏乡等地灾情较重,境内电力、通信暂时中断,目前汶川县至成都、理县方向道路均已中断。汶川三江泥石流是在2008年5月12日发生的。...
-

- 一亩地有多大概念图(一亩地大概是多大)
-
一亩=666.7平方米,五十亩=33335平方米55亩地相当于标准化的足球场2个半的大小。扩展资料:亩的古制换算井田制百步为亩(宽一步、长百步)。秦国商鞅变法废井田,以二百四十步为一亩。秦并六国,汉承秦制,大小亩并行。至汉武帝统一田亩步数,...
-
2026-01-13 08:12 alicucu
-
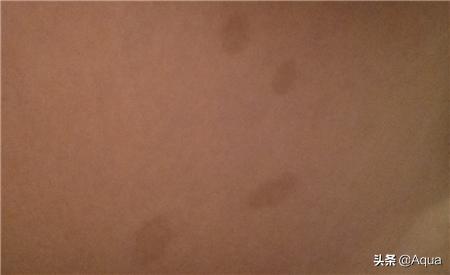
- 花斑癣图片(花斑癣图片头上)
-
出现花斑癣主要是由于真菌感染引起的,治疗过程当中可以采取一些涂抹药物来治疗,比如硝酸舍他康唑乳膏,同时在这期间也可以口服药物治疗,平时一定要注意饮食,尽量不要吃一些辣椒等食物,可以多补充一些水果和蔬菜,对病情是有好大帮助的,其次一定要去正规...
-
2026-01-13 07:59 alicucu
- 缺钙吃什么水果好(缺钙吃啥水果好)
-
补钙的水果是有很多的每天都吃一点都是很好的,香蕉,苹果,梨,还有菠萝等等都是含钙量很高的水果,除了吃水果外,补充一些含钙的食物也是非常好的1、橙子:橙子中含有丰富的维生素C,并且含有大量的钙离子。每五...
- 金钱鳘鱼胶一斤多少钱(小须金钱鳘鱼胶一斤多少钱)
-
血鳘鱼胶45头的价格约在950/一斤。这个价格算是比较接近批发价,市面上的价格可能比这个高200-300元左右,也就是1200-1300左右。花胶因为品种、产地、卖相、功能、存放年限和稀少程度的不同...
- particular是什么意思(particular)
-
不是在任何时候都通用的!在当尤其,特别的意思讲几乎通用。但especially还有专门地意思。eg:thiscrownwasmadeespeciallyfortheking.(这顶王冠是为国王特制的)...
- 全球电影票房榜前十名(全球电影票房榜前十名及国家)
-
片名票房预算年代1、复仇者联盟4:终局之战27亿9,780万3.56亿20192、阿凡达27亿9,044万2.37亿20093、泰坦尼克号21亿9,444万2亿19974、星球...
- 泰剧迷app粉色版(泰剧迷app粉色版官方安卓版下载)
-
可以通过以下步骤下载到电脑:1.首先在网上搜索粉色泰剧,找到可供下载的网站,例如迅雷下载、BT种子下载等;2.选择一个下载地址,点击下载链接,使用下载工具下载。3.等待下载完成后就可以...
- 盘多多网盘搜索(百度云搜索)
-
盘多多属于垂直搜索引擎;是类似百度网盘等的搜索引擎。特点是“专、精、深”,且具有行业色彩,相比较通用搜索引擎的海量信息无序化,垂直搜索引擎则显得更加专注、具体和深入。叮铃铃垂直搜索引擎为用户提供的并不...
- 大专生当兵回来直接专升本吗
-
如果您大专一年级的时候去当兵,当兵回来还是继续从大一读。那么,专科三年的话,加上专升本后本科学历是两年,全部学历是五年。一般当兵两年,大专3年,专升本2年,加一起7年,这是基本的时间可以,专科毕业当年...
- 被世界公认10大最好听的国歌
-
1.法国的马赛曲!2.美国国歌,3.俄罗斯国歌,4.意大利国歌,5.西班牙国歌,6.中国国歌,7.希腊国歌,8.葡萄牙国歌,9,英国国歌,10.德国国歌。个人感觉。客观的说,是前苏联的最好听,这是...
- 四川职业技术学院排名(四川职业技术学院排名前十公办)
-
四川排名前十的职业技术学院 1.四川建筑职业技术学院 2.四川工程职业技术学院 3.成都航空职业技术学院 ...
- 一周热门
- 最近发表
- 标签列表
-


