湖南长沙特产零食(长沙特产小食品有哪些)
alicucu 2025-12-21 21:47 2 浏览
1、长沙臭豆腐
长沙臭豆腐是湖南长沙传统的特色名吃,长沙当地人又称臭干子。色墨黑,外焦里嫩,鲜而香辣。 焦脆而不糊、细嫩而不腻、初闻臭气扑鼻,细嗅浓香诱人。
2、糖油粑粑
糖油粑粑,是湖南长沙市的地方传统名吃,糖油粑粑成本便宜,主要原料是糯米粉和糖,但其制造工艺精细讲究,有特殊的制造过程。
3、麻辣子鸡
麻辣子鸡始创于清朝同治年间,是具有浓厚地方风味的湘菜名肴之一。麻辣子鸡通常选用母仔鸡为主料百,配以辣椒为辅料,经食用油炼炒,再佐以绍酒、黄醋、大蒜等调料烹制而成。
4、口味虾
口味虾,又名麻辣小龙虾、长沙口味虾、香辣小龙虾等,是湖南省著名的传统小吃,以小龙虾制成,口味辣鲜香,色泽红亮,质地滑嫩,滋味香辣。
5、德园包子
德园包子是湖南长沙地区的传统小吃之一。选料精细,糖陷香甜爽口,肉陷则选用猪前夹缝肉或好瘦肉,拌以香菇、笋干、葱姜、冻油等度调料,油而不腻。
它们是:五娭毑臭豆腐,绝味鸭脖,问群锅饺,糖油粑粑,姊妹团子,口味虾,杨裕兴面食,刮凉粉,龙脂猪血,炖猪脚。
长沙十大零食:花片,牛皮糖,盐姜,炒米,辣条,酸枣糕,仁片糕,酱板鸭脖,毛毛鱼,秘制毛豆,酒鬼花生等等。还有茶颜悦色。
相关推荐
- 干燥剂有哪几种(食品干燥剂有哪几种)
-
1、酸性干燥剂:浓硫酸、P2O5、硅胶浓硫酸(强氧化性酸)、P2O5(酸性白色粉末)、硅胶(它是半透明,内表面积很大的多孔性固体,有良好的吸附性,对水有强烈的吸附作用。含有钴盐的硅胶叫变色硅胶,没有吸...
- 家用直饮水机(家用直饮水机十大名牌)
-
1、看直饮机是否有卫生许可证批件上所写的产品名字、型号要一致,因为即使在有证企业中,也存在“一证多用”的情况,即出现多个产品型号用一个卫生许可批件,消费者一定要查看清楚。2、看直饮机滤芯是否合适第一代...
- 滚筒洗衣机排行榜2025前十名
-
各有好处。1,上排水排的并不彻底,水泵处会有积水,要是放在特别冷的地方就需要在每次洗完衣服后动手给水泵排水。但也不会影响洗衣效果,因为有单向阀门限制水流向。但上排水在布置排水管时简单,上下都能排。2,...
- 世界美女排行榜前一百(世界美女排行榜100名2019)
-
2021年即将进入尾声,美国网站TCCandler每年都会选出全球百大美女排行榜,如今官方名单出炉,今年的第一名是韩国女团BLACKPINK的成员Lisa,去年是第二名。EmilieNereng今...
-
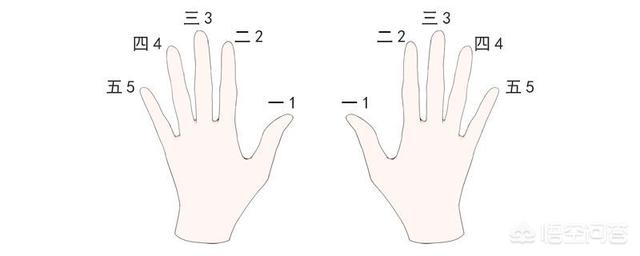
- 电子琴1234567指法图(1234567手势图)
-
尤克里里1234567的指法三弦空品是1,三弦二品是2,二弦空品是3,二弦一品是4,二弦三品是5,四弦空品也是5,一弦空品是6,四弦二品也是6,一弦二品是7。在弹奏尤克里里的时候要注意,手型是使用的古典手型,左手的一指左侧按琴弦,其余的手指...
-
2025-12-24 05:12 alicucu
- 长沙房产网(长沙房产网房天下)
-
长沙房地产公司排名1、湖南鑫远投资集团有限公司2、红星实业集团有限公司3、中建信和地产有限公司4、恒大地产集团长沙置业有限公司5、湖南保利房地产开发有限公司6、湖南天城置业发展有限公司7、长沙龙湖房地...
- 电子烟(电子烟有尼古丁吗)
-
电子烟是由中国人发明的,这个毋庸置疑。多数资料及实验显示。电子烟除尼古丁之外没有发现其他任何有害成分,对人体的不利影响也低于传统香烟。原材料不同:电子烟是微电子科技产品,有雾化器、锂电池和烟弹。目前市...
- 今年最流行的头发造型(今年最流行的头发造型和颜色)
-
时尚流行和个人喜好是选择头发颜色时需要考虑的因素,不过每年的流行趋势都会有所不同,以下列举几种近年来比较受欢迎的头发颜色:1.灰棕色:灰棕色是一种既低调又独特的中性色调,适合许多不同的肤色和发质,也非...
- 榴莲吃不完冷藏还是冷冻(榴莲冷冻的正确方法)
-
吃不完榴莲肉大多数可以冷冻,冷冻过后可能口感上会有一些差异,但是里面营养物质并不会流失,可以在吃时候解冻。但是避免长时间的冷冻,也会导致营养价值降低。榴莲的保存一般是冷冻比较好,而且可以存放的时间比较...
-

- 北京四达烂校211(北京四达国际)
-
没有最差的211之说,能被评为211大学都是有过硬的学术研究和科研能力。大学是教书育人的地方不是进行攀比名气的场所首先,北京语言大学身处首都,占据地理优势,另外这个学校虽然不是双一流学校,不是211学校,但是有些专业很不错,尤其是小语种,而...
-
2025-12-24 02:59 alicucu
- 龙的英文(龙的英文gala)
-
dragon读音:英[?dr?g?n]美[?dr?ɡ?n]n.龙,龙船;[D-][天文学]天龙(星座);[口语、贬义]脾气暴躁的人复数:dragons例句:1、Later,drag...
-

- 网线颜色顺序(网线颜色顺序水晶头)
-
网线颜色的顺序是有相应的标准的!TIA568B/568B就是!我们现在用的是TIA568B的标准!在以前的计算机网卡或是集线器,路由器,交换机等并不支持网线发送和接受的自动翻转!这就需要两个标准,同设备间做手动翻转来使两个设备可以通讯!比如...
-
2025-12-24 01:59 alicucu
- 芈月母亲向氏历史原型(芈月母亲向氏历史原型是谁)
-
芈月母亲向氏是莒姬宫里的媵女,因生育芈月被封为向夫人,后因生育芈戎被封为向妃。后来因为被王后趁大王不在诬陷她染上恶疾被赶出宫,被贱兵魏甲玷污,后来生下魏冉。大王回宫后接向妃回宫,为了给芈月芈戎换的好前...
- 天蝎座女生床上太可怕了(天蝎座女孩子床上的表现)
-
根据推断白羊配天蝎床会塌,这是根据星座之间的搭配得出的一种学说结论,因为白羊和天蝎两种人的性格是完全矛盾的,所以在结合之后会导致床塌
- 七情六欲代表什么意思(七情六欲什么意思呀)
-
七情六欲 七情,指一般人所具有之七种感情:喜、怒、忧、思、悲、恐、惊。六欲指眼、耳、鼻、舌、身、意六欲。 七情六欲,七情是指喜、怒、忧、思、悲、恐、惊。的感情表现或心理运动;六欲是指人的...
- 一周热门
- 最近发表
- 标签列表
-


