南怀瑾对未来的惊人预言(南怀瑾的100句预言)
alicucu 2026-01-12 15:59 1 浏览
是说的紫薇圣人吧,在古代与近代很多预言里都提到紫薇圣人,如果从现代和平年代来说,不能说是最强。如果从社会发展来说,在和平年代的话,最发达的就是经济:艺术:文化。紫薇圣人,就是引领人类思想发生巨大转变,人生价值观,世界观发生根本性改变,适应社会需要,也可以说是必然出现的人。
预言中的紫圣是,紫圣天君。
- 上一篇:世界最大航母有多大
- 下一篇:2019春晚直播回放(2019年春晚直播回放)
相关推荐
- 朱姆沃尔特级驱逐舰(朱姆沃尔特级驱逐舰参数)
-
朱姆沃尔特驱逐舰于2016年10月15日正式加入美国海军服役!
- 男士护肤品套装十大排行榜(男士护肤品套装哪个牌子好)
-
碧欧泉男士水动力套装这套护肤套装畅销很多年了,套装颜值很高,看外表就知道走的是高端路线。专研男士保湿的套装,洗面奶添加透明颤菌发酵物,保湿感足洗完不紧绷,还有薄荷醇,用起来很清凉,洗面奶味道也很好闻。...
-

- 2019春晚直播回放(2019年春晚直播回放)
-
1.开场歌舞《万紫千红中国年》表演:容祖儿、周渝民、陈晓、佟丽娅、胡可、沙溢、安吉、小鱼儿...2.歌舞《我的春晚我的年》表演:张曼玉、王凯、杨洋、空军蓝天幼儿园3.相声《我爱诗词》表演:冯巩、贾旭明、曹随风、侯林林4.歌曲《中国》...
-
2026-01-12 16:12 alicucu
- 南怀瑾对未来的惊人预言(南怀瑾的100句预言)
-
是说的紫薇圣人吧,在古代与近代很多预言里都提到紫薇圣人,如果从现代和平年代来说,不能说是最强。如果从社会发展来说,在和平年代的话,最发达的就是经济:艺术:文化。紫薇圣人,就是引领人类思想发生巨大转变,...
- 世界最大航母有多大
-
加贺,现在也不贵,8级航母中t0的存在,那机库量应该是全部航母中最高的,可以任你去浪,就算不小心一波团灭问题也不大,并且还拥有8级航母中单组鱼雷机伤害最高,一波差不多能刮下来1万7左右的伤害,碰到6级...
- 海南大学研究生招生简章(海南医学院研究生招生简章)
-
收2021年,海南大学收法专研究生共计82人,海南大学,这是我们国家的一所非常优秀的大学,海南大学手法专业的研究生在我们国家同类大学当中享有姓名,很多报考研究生了,大学生都把海南大学手法专业研究生作为...
-
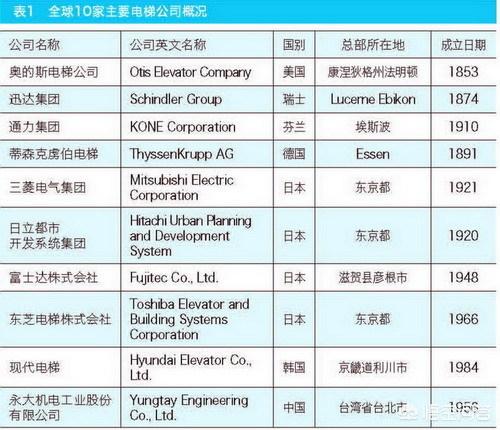
- 电梯公司(电梯公司排名)
-
依据2013年世界电梯企业销售额排名,世界十大电梯企业分别为:1.奥的斯电梯公司(美国奥的斯电梯),销售额124.84亿美元;2.迅达集团(瑞士迅达电梯),销售额98.95亿美元;3.通力集团(芬兰通力电梯),销售额95.51亿美元;4.蒂...
-
2026-01-12 14:12 alicucu
- 巨人骸骨是真的吗(巨人骸骨之谜)
-
不真实因为根据考古学家的研究,目前没有发现任何关于22米巨人的实物证据,而且这种巨大体型的生物也不符合生物学规律。此外,网络上也有很多关于22米巨人的虚假信息和谣言,因此可以判断这只是一个虚假的传说或...
- 宝宝米粉哪个牌子口碑最好(宝宝米粉哪种好)
-
不知道其他宝妈们都选的哪一款,我是给宝宝吃的嘉宝米粉,因为我发现各大米粉的排行榜中都有这个牌子,现在宝宝吃了一年多了,各方面的表现都非常棒,没有辜负我的信任。它的营养非常好,各种宏量营养素和微量营养素...
- 适合玩游戏的手机(适合玩游戏的手机2000到3000)
-
您好想要一款最适合玩游戏的手机说法不一其实在于这个最字是值多少钱要说玩游戏苹果系列的是没得说的安卓再好游戏对比下来还是有点差距2000元价位:推荐红米k20p3000元价位:oppoace40...
- 蓝色最佳配色表(国风蓝色最佳配色表)
-
蓝色是一种冷色调,搭配起来有很多选择。与白色搭配,会增加整体的清新感和简洁感;与深灰色搭配,会增加低调稳重的感觉;与深紫色搭配,会呈现神秘感和高贵感;与淡黄色搭配,会营造出温暖和谐的氛围。总的来说,蓝...
- 关切的近义词(关心关切的近义词)
-
1、关切的反义词是:冷漠、冷淡、淡漠、漠视、无视。关切词语解释【拼音】:[guānqiè]【释义】:1.关系,关连。2.关系密切。3.关心。4.亲切。2、真理的反义词是:谬论、邪说、谬误真理词语解释...
- 张厚载(张厚载的原型是谁)
-
结局:《觉醒年代》第二十集中,国会召集罢免蔡元培北大校长职务的听证会。会议议程已经开始,而提交议案的易夔龙议员却没有出现。议案的第二提议人张长礼建议绕过质询和辩论环节,直接开始投票表决。北大师生一片哗...
- 日用品批发市场进货(日用品批发市场进货地址在哪里)
-
一般而言,大家首先想到的都是在小商品市场进货。而全国散货百货店进货大都来自义乌,是国内最大的小商品批发市场,10元的商品利润基本都可以保证一半左右。义乌批发市场几乎囊括了工艺品、饰品百货、箱包雨具、电...
- 一周热门
- 最近发表
- 标签列表
-


